ps Namespace Reference

Classes
struct	GridND
struct	Point
	A fixed-size N-dimensional point/vector class. More...
struct	PointCloudAdaptor

Typedefs
template<typename T , size_t N>
using	KDTree = nanoflann::KDTreeSingleIndexAdaptor< nanoflann::L2_Simple_Adaptor< T, PointCloudAdaptor< T, N > >, PointCloudAdaptor< T, N >, N >

Functions
template<typename T , size_t N>
std::vector< int >	dbscan_clustering (const std::vector< Point< T, N > > &points, T eps, size_t min_pts)
	Density-Based Spatial Clustering of Applications with Noise (DBSCAN).
template<typename T , std::size_t N>
std::vector< Point< T, N > >	distance_rejection_filter (const std::vector< Point< T, N > > &points, T min_dist)
	Filters a set of points using a greedy distance-based rejection.
template<typename T , std::size_t N, typename ScaleFn >
std::vector< Point< T, N > >	distance_rejection_filter_warped (const std::vector< Point< T, N > > &points, T base_min_dist, ScaleFn scale_fn)
	Filters points based on spatially-varying minimal distance constraints.
template<typename T , size_t N, typename DensityFn >
std::vector< Point< T, N > >	function_rejection_filter (const std::vector< Point< T, N > > &points, DensityFn density_fn, std::optional< unsigned int > seed=std::nullopt)
	Filters points based on a spatial probability (density) function.
template<typename T , size_t N>
std::vector< Point< T, N > >	gaussian_clusters (std::vector< Point< T, N > > cluster_centers, size_t points_per_cluster, T spread, std::optional< unsigned int > seed=std::nullopt)
	Generates clustered points around provided cluster centers using a Gaussian distribution.
template<typename T , size_t N>
std::vector< Point< T, N > >	gaussian_clusters (size_t cluster_count, size_t points_per_cluster, const std::array< std::pair< T, T >, N > &axis_ranges, T spread, std::optional< unsigned int > seed=std::nullopt)
	Generates clustered points around random centers uniformly sampled in a bounding box.
template<typename T , size_t N>
std::vector< Point< T, N > >	halton_sequence (size_t count, size_t shift)
template<typename T , size_t N>
std::vector< Point< T, N > >	halton (size_t count, const std::array< std::pair< T, T >, N > &axis_ranges, std::optional< unsigned int > seed=std::nullopt)
	Generates a set of quasi-random points using the Halton sequence in N dimensions.
template<typename T , size_t N>
std::vector< Point< T, N > >	hammersley_sequence (size_t count, size_t shift)
template<typename T , size_t N>
std::vector< Point< T, N > >	hammersley (size_t count, const std::array< std::pair< T, T >, N > &axis_ranges, std::optional< unsigned int > seed=std::nullopt)
	Generates a set of quasi-random points using the Hammersley sequence in N dimensions.
template<typename T , size_t N, typename DensityFn >
std::vector< Point< T, N > >	importance_resampling (size_t count, size_t oversampling_ratio, const std::array< std::pair< T, T >, N > &axis_ranges, DensityFn density_fn, std::optional< unsigned int > seed=std::nullopt)
	Generates a point set via importance resampling from a quasi-random oversampled grid.
template<typename T , size_t N>
std::vector< Point< T, N > >	jittered_grid (size_t count, const std::array< std::pair< T, T >, N > &axis_ranges, const std::array< T, N > &jitter_amount, const std::array< T, N > &stagger_ratio, std::optional< unsigned int > seed=std::nullopt)
	Generates a point set on a jittered and optionally staggered grid.
template<typename T , size_t N>
std::vector< Point< T, N > >	jittered_grid (size_t count, const std::array< std::pair< T, T >, N > &axis_ranges, std::optional< unsigned int > seed=std::nullopt)
	Generates a jittered grid of points with full jitter and no stagger.
template<typename T , size_t N>
std::pair< std::vector< Point< T, N > >, std::vector< size_t > >	kmeans_clustering (const std::vector< Point< T, N > > &points, size_t k_clusters, bool normalize_data=true, size_t max_iterations=100)
	Perform k-means clustering on a set of points.
template<typename T , std::size_t N>
std::vector< Point< T, N > >	latin_hypercube_sampling (std::size_t sample_count, const std::array< std::pair< T, T >, N > &axis_ranges, std::optional< unsigned int > seed=std::nullopt)
	Generates samples using Latin Hypercube Sampling (LHS).
template<typename T , size_t N>
std::pair< std::vector< T >, std::vector< T > >	angle_distribution_neighbors (const std::vector< Point< T, N > > &points, T bin_width, size_t k_neighbors=8)
	Compute the angular distribution function (ADF) using nearest neighbors.
template<typename T , size_t N>
std::vector< T >	distance_to_boundary (const std::vector< Point< T, N > > &points, const std::array< std::pair< T, T >, N > &axis_ranges)
	Compute the distance of each point to the domain boundary.
template<typename T , size_t N>
std::vector< T >	first_neighbor_distance_squared (std::vector< Point< T, N > > &points)
	Computes the squared distance to the nearest neighbor for each point.
template<typename T , size_t N>
std::vector< T >	local_density_knn (const std::vector< Point< T, N > > &points, size_t k=8)
	Compute local point density based on k-nearest neighbors in N dimensions.
template<typename T , size_t N>
std::vector< std::vector< size_t > >	nearest_neighbors_indices (const std::vector< Point< T, N > > &points, size_t k_neighbors=8)
	Finds the nearest neighbors for each point in a set.
template<typename T , size_t N>
std::pair< std::vector< T >, std::vector< T > >	radial_distribution (const std::vector< Point< T, N > > &points, const std::array< std::pair< T, T >, N > &axis_ranges, T bin_width, T max_distance)
	Compute the normalized radial distribution function g(r).
template<typename T , size_t N>
std::vector< int >	percolation_clustering (const std::vector< Point< T, N > > &points, T connection_radius)
	Analyze percolation clusters from a set of points using a radius-based neighbor graph.
template<typename T , size_t N>
Point< T, N >	operator+ (const Point< T, N > &a, const Point< T, N > &b)
template<typename T , size_t N>
Point< T, N >	operator- (const Point< T, N > &a, const Point< T, N > &b)
template<typename T , size_t N>
Point< T, N >	operator* (const Point< T, N > &a, const Point< T, N > &b)
template<typename T , size_t N>
Point< T, N >	operator/ (const Point< T, N > &a, const Point< T, N > &b)
template<typename T , size_t N>
Point< T, N >	operator+ (const Point< T, N > &p, T scalar)
template<typename T , size_t N>
Point< T, N >	operator- (const Point< T, N > &p, T scalar)
template<typename T , size_t N>
Point< T, N >	operator* (const Point< T, N > &p, T scalar)
template<typename T , size_t N>
Point< T, N >	operator/ (const Point< T, N > &p, T scalar)
template<typename T , size_t N>
Point< T, N >	operator* (T scalar, const Point< T, N > &p)
template<typename T , size_t N>
Point< T, N >	operator+ (T scalar, const Point< T, N > &p)
template<typename T , size_t N>
T	dot (const Point< T, N > &a, const Point< T, N > &b)
template<typename T , size_t N>
T	length_squared (const Point< T, N > &a)
template<typename T , size_t N>
T	length (const Point< T, N > &a)
template<typename T , size_t N>
Point< T, N >	normalized (const Point< T, N > &a)
template<typename T , size_t N>
T	distance_squared (const Point< T, N > &a, const Point< T, N > &b)
template<typename T , size_t N>
T	distance (const Point< T, N > &a, const Point< T, N > &b)
template<typename T , size_t N>
Point< T, N >	lerp (const Point< T, N > &a, const Point< T, N > &b, T t)
template<typename T , size_t N>
Point< T, N >	clamp (const Point< T, N > &p, T min_val, T max_val)
template<typename T , size_t N, typename ScaleFn >
bool	in_neighborhood (const GridND< T, N > &grid, const Point< T, N > &p, T base_min_dist, const std::array< std::pair< T, T >, N > &ranges, ScaleFn scale_fn)
template<typename T , size_t N>
Point< T, N >	generate_random_point_around (const Point< T, N > &center, T base_min_dist, std::mt19937 &gen, std::function< T(const Point< T, N > &)> scale_fn)
template<typename T , size_t N, typename ScaleFn >
std::vector< Point< T, N > >	poisson_disk_sampling (size_t count, const std::array< std::pair< T, T >, N > &ranges, T base_min_dist, ScaleFn scale_fn, std::optional< unsigned int > seed=std::nullopt, size_t new_points_attempts=30)
	Generate a set of Poisson disk samples in N-dimensional space, possibly with a warped metric.
template<typename T , size_t N>
std::vector< Point< T, N > >	poisson_disk_sampling_uniform (size_t count, const std::array< std::pair< T, T >, N > &ranges, T base_min_dist, std::optional< unsigned int > seed=std::nullopt, size_t new_points_attempts=30)
	Generate uniformly distributed Poisson disk samples in N-dimensional space.
template<typename T , size_t N, typename RadiusGen >
std::vector< Point< T, N > >	poisson_disk_sampling_distance_distribution (size_t n_points, const std::array< std::pair< T, T >, N > &axis_ranges, RadiusGen &&radius_gen, std::optional< unsigned int > seed=std::nullopt, size_t max_attempts=30)
	Generate random points with a variable-radius Poisson disk sampling.
template<typename T , size_t N>
std::vector< Point< T, N > >	poisson_disk_sampling_power_law (size_t n_points, T dist_min, T dist_max, T alpha, const std::array< std::pair< T, T >, N > &axis_ranges, std::optional< unsigned int > seed=std::nullopt, size_t max_attempts=30)
	Generate N-dimensional points using Poisson disk sampling with a power-law radius distribution.
template<typename T , size_t N>
std::vector< Point< T, N > >	poisson_disk_sampling_weibull (size_t n_points, T lambda, T k, const std::array< std::pair< T, T >, N > &axis_ranges, std::optional< unsigned int > seed=std::nullopt, size_t max_attempts=30)
	Generate N-dimensional points using Poisson disk sampling with a Weibull-distributed radius.
template<typename T , size_t N>
std::vector< Point< T, N > >	poisson_disk_sampling_weibull (size_t n_points, T lambda, T k, T dist_min, const std::array< std::pair< T, T >, N > &axis_ranges, std::optional< unsigned int > seed=std::nullopt, size_t max_attempts=30)
	Poisson disk sampling in N dimensions with radii drawn from a Weibull distribution, enforcing a minimum exclusion distance.
template<typename T , size_t N>
std::vector< Point< T, N > >	random (size_t count, const std::array< std::pair< T, T >, N > &axis_ranges, std::optional< unsigned int > seed=std::nullopt)
	Generates a specified number of uniformly distributed random points in N-dimensional space.
template<typename T , std::size_t N>
std::vector< Point< T, N > >	random_rejection_filter (const std::vector< Point< T, N > > &points, std::size_t target_count)
	Randomly retains a fixed number of points from the input set.
template<typename T , std::size_t N>
std::vector< Point< T, N > >	random_rejection_filter (const std::vector< Point< T, N > > &points, float keep_fraction)
	Randomly retains a fraction of the input points.
template<typename T , size_t N>
std::vector< Point< T, N > >	random_walk_filaments (size_t n_filaments, size_t filament_count, T step_size, const std::array< std::pair< T, T >, N > &ranges, std::optional< unsigned int > seed=std::nullopt, T persistence=T(0.8), T gaussian_sigma=T(0), size_t gaussian_samples=0, std::vector< T > *p_distances=nullptr)
	Generate random walk filaments in N dimensions with optional Gaussian thickness.
template<typename T , size_t N>
std::vector< Point< T, N > >	filter_points_in_range (const std::vector< Point< T, N > > &points, const std::array< std::pair< T, T >, N > &axis_ranges)
	Filters points that lie within the specified axis-aligned bounding box.
template<typename T , std::size_t N, typename Func >
std::vector< Point< T, N > >	filter_points_function (const std::vector< Point< T, N > > &points, Func fn)
	Filters points using a user-provided function.
template<typename T , size_t N>
void	refit_points_to_range (std::vector< Point< T, N > > &points, const std::array< std::pair< T, T >, N > &target_ranges)
	Linearly remap a set of points to fit within the specified axis-aligned ranges.
template<typename T , size_t N>
void	rescale_points (std::vector< Point< T, N > > &points, const std::array< std::pair< T, T >, N > &ranges)
	Rescales normalized points (in [0, 1]) to specified axis-aligned ranges.
template<typename T , size_t N, typename DensityFn >
std::vector< Point< T, N > >	rejection_sampling (size_t count, const std::array< std::pair< T, T >, N > &axis_ranges, DensityFn density_fn, std::optional< unsigned int > seed=std::nullopt)
	Generates random points using rejection sampling based on a user-defined density function.
template<typename T , size_t N>
void	relaxation_ktree (std::vector< Point< T, N > > &points, size_t k_neighbors=8, T step_size=T(0.1), size_t iterations=10)
	Relax a point set using a k-nearest neighbor repulsion algorithm with a KD-tree.
template<typename T , size_t N>
bool	save_points_to_csv (const std::string &filename, const std::vector< Point< T, N > > &points, bool write_header=true)
	Save a set of N-dimensional points to a CSV file.
template<typename T >
bool	save_vector_to_csv (const std::string &filename, const std::vector< T > &values, bool write_header=true, const std::string &header_name="value")
	Save a 1D vector of values to a CSV file.
template<typename T , size_t N>
std::vector< Point< T, N+1 > >	add_dimension (const std::vector< Point< T, N > > &points, const std::vector< T > &new_dimension)
	Add a new dimension to a set of points.
template<typename T , size_t N>
std::vector< std::vector< Point< T, N > > >	extract_clusters (const std::vector< Point< T, N > > &points, const std::vector< int > &labels)
	Extract clusters of points given DBSCAN (or any clustering) labels.
template<typename T , size_t N>
std::vector< Point< T, N > >	merge_by_dimension (const std::array< std::vector< T >, N > &components)
	Reconstructs a list of N-dimensional points from N separate coordinate vectors.
template<typename T , size_t N>
void	normalize_points (std::vector< Point< T, N > > &points)
	Normalize the coordinates of a set of points along each axis to the range [0, 1].
template<typename T , size_t N>
std::array< std::vector< T >, N >	split_by_dimension (const std::vector< Point< T, N > > &points)
	Rearranges a list of N-dimensional points into N separate coordinate vectors.

Typedef Documentation

KDTree

template<typename T , size_t N>

using ps::KDTree = typedef nanoflann::KDTreeSingleIndexAdaptor< nanoflann::L2_Simple_Adaptor<T, PointCloudAdaptor<T, N> >, PointCloudAdaptor<T, N>, N>

Function Documentation

add_dimension()

template<typename T , size_t N>

std::vector< Point< T, N+1 > > ps::add_dimension	(	const std::vector< Point< T, N > > &	points,
		const std::vector< T > &	new_dimension
	)

Add a new dimension to a set of points.

This function takes a vector of points of dimension N and appends a new coordinate to each point, producing a new vector of points of dimension N+1.

Template Parameters

T	Numeric type of the coordinates (e.g., float, double, int).
N	Current number of dimensions in the input points.

Parameters

points	Vector of input points of dimension N.
new_dimension	Vector of values for the new dimension. Must have the same size as points.

Returns

A vector of points of dimension N+1, with the new dimension appended.

Exceptions

std::runtime_errorifthesizeof`points`and`new_dimension`donotmatch.

Note

This function creates a new vector of points with an increased dimension count, since the type Point<T, N> is distinct from Point<T, N+1>.

Example

std::vector<Point<float, 2>> points = { {{1.0f, 2.0f}}, {{3.0f, 4.0f}}};
std::vector<float> z_values = { 10.0f, 20.0f };
auto points3D = add_dimension(points, z_values);
// points3D now contains {{1.0f, 2.0f, 10.0f}}, {{3.0f, 4.0f, 20.0f}}

angle_distribution_neighbors()

template<typename T , size_t N>

std::pair< std::vector< T >, std::vector< T > > ps::angle_distribution_neighbors	(	const std::vector< Point< T, N > > &	points,
		T	bin_width,
		size_t	k_neighbors = 8
	)

Compute the angular distribution function (ADF) using nearest neighbors.

The angular distribution function (ADF) measures the distribution of bond angles formed by a point and pairs of its nearest neighbors.

• Flat distribution → random uniform points.
• Peaks at characteristic angles → local order (e.g. hexagonal lattice peaks at 60°).
• Depletions → angular avoidance due to constraints or repulsion.

Template Parameters

T	Numeric type (float, double, ...)
N	Dimension of points (N >= 2)

Parameters

points	Vector of points
bin_width	Width of angle bins (in radians)
k_neighbors	Number of neighbors used for angle calculation (default: 8)

Returns

std::pair<std::vector<T>, std::vector<T>>

• First: bin centers (angles in radians)
• Second: normalized ADF values

Example

std::vector<Point<double, 2>> pts = {
    {0.0, 0.0}, {1.0, 0.0}, {0.0, 1.0}, {1.0, 1.0}
};
 
auto [theta, g_theta] = angle_distribution_neighbors(pts, 0.1, 6);
 
for (size_t i = 0; i < theta.size(); ++i)
  std::cout << "θ=" << theta[i] << "g(θ)=" << g_theta[i] << std::endl;

clamp()

template<typename T , size_t N>

Point< T, N > ps::clamp	(	const Point< T, N > &	p,
		T	min_val,
		T	max_val
	)

dbscan_clustering()

template<typename T , size_t N>

std::vector< int > ps::dbscan_clustering	(	const std::vector< Point< T, N > > &	points,
		T	eps,
		size_t	min_pts
	)

Density-Based Spatial Clustering of Applications with Noise (DBSCAN).

Groups points into clusters based on density: a point is a core if it has at least min_pts neighbors within distance eps. Clusters are formed by expanding from core points. Noise points remain unclustered.

Template Parameters

T	Scalar type (float/double).
N	Dimension.

Parameters

points	Input point cloud.
eps	Neighborhood radius for density check.
min_pts	Minimum neighbors (including self) to be a core point.

Returns

A vector of cluster labels (-1 = noise, 0..k = cluster IDs).

Example

auto labels = dbscan<double,2>(points, 0.05, 5);

This assigns each 2D point either to a cluster ID or -1 (noise).

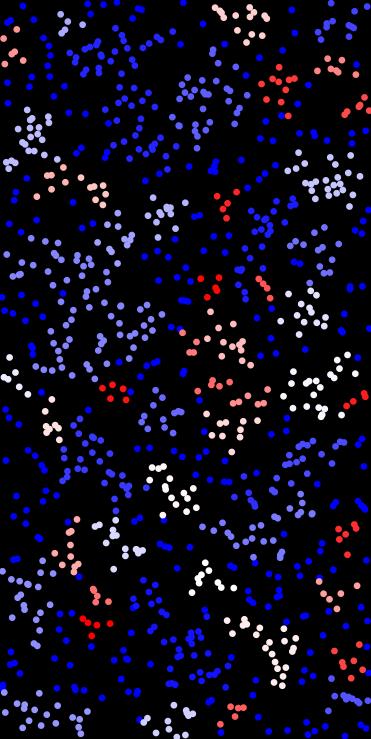
distance()

template<typename T , size_t N>

T ps::distance	(	const Point< T, N > &	a,
		const Point< T, N > &	b
	)

distance_rejection_filter()

template<typename T , std::size_t N>

std::vector< Point< T, N > > ps::distance_rejection_filter	(	const std::vector< Point< T, N > > &	points,
		T	min_dist
	)

Filters a set of points using a greedy distance-based rejection.

Points are added one by one. If a point is at least min_dist away from all previously accepted points, it is kept. Otherwise, it is rejected.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

points	Vector of candidate points
min_dist	Minimum allowed distance between two accepted points

Returns

std::vector<Point<T, N>> of filtered points

Example

std::vector<Point<float, 2>> pts = ps::random<float, 2>(1000, {{0,1},{0,1}});
auto filtered = ps::distance_rejection_filter(pts, 0.05f);

distance_rejection_filter_warped()

template<typename T , std::size_t N, typename ScaleFn >

std::vector< Point< T, N > > ps::distance_rejection_filter_warped	(	const std::vector< Point< T, N > > &	points,
		T	base_min_dist,
		ScaleFn	scale_fn
	)

Filters points based on spatially-varying minimal distance constraints.

A scale function is used to modulate the minimum allowed distance for each point. The base distance base_min_dist is scaled by the value returned by scale_fn(p), allowing for adaptive sampling densities.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space
ScaleFn	Callable returning a scalar scale factor for a given point

Parameters

points	Vector of candidate points
base_min_dist	Base minimum allowed distance
scale_fn	Function providing a local scale factor per point

Returns

std::vector<Point<T, N>> A filtered set of points with variable spacing

Example

auto scale_fn = [](const Point<float, 2>& p) {
    return 0.5f + 0.5f * std::sin(p[0] * 3.1415f); // Varies between 0.5 and 1
};
 
std::vector<Point<float, 2>> pts = ps::random<float, 2>(1000, {{0,1},{0,1}});
auto filtered = ps::distance_rejection_filter_warped(pts, 0.05f, scale_fn);

distance_squared()

template<typename T , size_t N>

T ps::distance_squared	(	const Point< T, N > &	a,
		const Point< T, N > &	b
	)

distance_to_boundary()

template<typename T , size_t N>

std::vector< T > ps::distance_to_boundary	(	const std::vector< Point< T, N > > &	points,
		const std::array< std::pair< T, T >, N > &	axis_ranges
	)

Compute the distance of each point to the domain boundary.

The domain is defined by axis-aligned ranges in each dimension. For each point, the returned distance is the smallest Euclidean distance to any boundary plane of the domain.

Template Parameters

T	Floating point type.
N	Dimensionality of the points.

Parameters

points	Vector of points to evaluate.
axis_ranges	Vector of size N, where each element is a std::pair<min, max> defining the domain limits in that dimension.

Returns

std::vector<T> Distances of each point to the nearest domain boundary.

Note

This assumes the domain is a rectangular box aligned with the coordinate axes.

Example

std::vector<Point<double, 2>> pts = { {0.2, 0.8}, {0.9, 0.1} };
std::vector<std::pair<double, double>> ranges = { {0.0, 1.0}, {0.0, 1.0} };
auto distances = distance_to_boundary(pts, ranges);
// distances[0] -> 0.2
// distances[1] -> 0.1

dot()

template<typename T , size_t N>

T ps::dot	(	const Point< T, N > &	a,
		const Point< T, N > &	b
	)

extract_clusters()

template<typename T , size_t N>

std::vector< std::vector< Point< T, N > > > ps::extract_clusters	(	const std::vector< Point< T, N > > &	points,
		const std::vector< int > &	labels
	)

Extract clusters of points given DBSCAN (or any clustering) labels.

Template Parameters

T	Scalar type.
N	Dimension.

Parameters

points	Input point cloud.
labels	Cluster labels (-2 = noise, -1 = unvisited, 0..k = cluster IDs).

Returns

A vector of clusters, each cluster is a vector of points.

Example

auto labels   = dbscan<double,2>(points, 0.05, 5);
auto clusters = extract_clusters(points, labels);

filter_points_function()

template<typename T , std::size_t N, typename Func >

std::vector< Point< T, N > > ps::filter_points_function	(	const std::vector< Point< T, N > > &	points,
		Func	fn
	)

Filters points using a user-provided function.

Keeps only the points for which the provided function fn(p) does not return zero. This can be used to apply custom masks, implicit surface functions, etc.

Template Parameters

T	Numeric type for coordinates.
N	Number of dimensions.
Func	Callable that takes a Point<T, N> and returns a value convertible to T.

Parameters

points	Vector of input points.
fn	Unary function that returns a non-zero value if the point should be kept.

Returns

A vector of filtered points.

std::vector<Point<float, 2>> pts = { {0.f, 0.f}, {1.f, 1.f}, {2.f, 2.f}};
auto lambda = [](const Point<float, 2> &p) {
    return (p[0] + p[1] < 2.5f) ? 1.f : 0.f;
};
auto filtered = ps::filter_points_function<float, 2>(pts, lambda);
// Keeps only { {0.f, 0.f}, {1.f, 1.f} }

filter_points_in_range()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::filter_points_in_range	(	const std::vector< Point< T, N > > &	points,
		const std::array< std::pair< T, T >, N > &	axis_ranges
	)

Filters points that lie within the specified axis-aligned bounding box.

Template Parameters

T	Numeric type for coordinates (e.g., float or double).
N	Number of dimensions.

Parameters

points	Vector of input points to filter.
axis_ranges	Axis-aligned bounding box ranges for each dimension (inclusive).

Returns

A vector containing only the points that lie within all specified axis ranges.

Exceptions

std::invalid_argumentifaxis_rangesareill-formed(e.g.,min

> max).

std::vector<Point<float, 2>> pts = { {0.5f, 0.5f}, {2.f, 3.f}, {-1.f, 0.f} };
auto filtered = ps::filter_points_in_range<float, 2>(pts, {{{0.f, 1.f},
                                                           {0.f, 1.f}}});
// filtered now contains only { {0.5f, 0.5f} }

first_neighbor_distance_squared()

template<typename T , size_t N>

std::vector< T > ps::first_neighbor_distance_squared

(

std::vector< Point< T, N > > &

points

)

Computes the squared distance to the nearest neighbor for each point.

This function builds a KD-tree from a given set of N-dimensional points and computes, for each point, the squared distance to its closest neighbor.

The KD-tree search uses nanoflann for efficient nearest neighbor queries.

Template Parameters

T	Scalar type (e.g., float, double).
N	Dimension of each point.

Parameters

points

Vector of N-dimensional points. Note:** This vector is passed by non-const reference because the KD-tree adaptor may require mutable access, but the function does not modify the contents.

Returns

A vector containing the squared distances to the first neighbor for each point, in the same order as the input points.

// Example usage:
#include <array>
#include <vector>
 
using Point3f = Point<float, 3>;
 
std::vector<Point3f> points = {
    {0.0f, 0.0f, 0.0f},
    {1.0f, 0.0f, 0.0f},
    {0.0f, 1.0f, 0.0f},
    {1.0f, 1.0f, 0.0f}
};
 
std::vector<float> distances_sq = first_neighbor_distance_squared(points);
 
// distances_sq[i] contains the squared distance to the closest neighbor of points[i].

function_rejection_filter()

template<typename T , size_t N, typename DensityFn >

std::vector< Point< T, N > > ps::function_rejection_filter	(	const std::vector< Point< T, N > > &	points,
		DensityFn	density_fn,
		std::optional< unsigned int >	seed = std::nullopt
	)

Filters points based on a spatial probability (density) function.

Each point is accepted with a probability given by density_fn(p), which should return a value in [0, 1]. This is useful for sampling from a non-uniform spatial distribution.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space
DensityFn	Callable type with signature T(const Point<T, N>&)

Parameters

points	Input candidate points
density_fn	Function returning acceptance probability for each point
seed	Optional random seed for reproducibility

Returns

std::vector<Point<T, N>> of accepted points

auto field = [](const Point<float, 2>& p) {
    return 0.5f + 0.5f * std::sin(p[0] * 10.0f); // Spatial density
};
auto accepted = ps::function_rejection_filter(pts, field);

gaussian_clusters() [1/2]

template<typename T , size_t N>

std::vector< Point< T, N > > ps::gaussian_clusters	(	size_t	cluster_count,
		size_t	points_per_cluster,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		T	spread,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates clustered points around random centers uniformly sampled in a bounding box.

Cluster centers are randomly sampled within the provided axis_ranges, and each cluster then has points_per_cluster points sampled from a Gaussian distribution centered at the cluster's location, with a specified standard deviation spread.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

cluster_count	Number of cluster centers to generate
points_per_cluster	Number of points per cluster
axis_ranges	Axis-aligned bounding box ranges for each dimension
spread	Standard deviation of the Gaussian spread
seed	Optional random seed

Returns

std::vector<Point<T, N>> A vector of clustered points

Example

 auto clustered = ps::gaussian_clusters<float, 2>(
    5, 100,
    {{{0,1}, {0,1}}}, 0.03f
);

gaussian_clusters() [2/2]

template<typename T , size_t N>

std::vector< Point< T, N > > ps::gaussian_clusters	(	std::vector< Point< T, N > >	cluster_centers,
		size_t	points_per_cluster,
		T	spread,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates clustered points around provided cluster centers using a Gaussian distribution.

For each cluster center, this function generates points_per_cluster points where each coordinate is sampled from a normal distribution centered at the coordinate of the cluster center with standard deviation spread.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

cluster_centers	A vector of cluster center points
points_per_cluster	Number of points to generate per cluster
spread	Standard deviation of the Gaussian spread
seed	Optional random seed

Returns

std::vector<Point<T, N>> A vector of clustered points

Example

std::vector<Point<float, 2>> centers = {
    {0.2f, 0.2f},
    {0.8f, 0.8f}
};
auto clustered = ps::gaussian_clusters(centers, 100, 0.05f);

generate_random_point_around()

template<typename T , size_t N>

Point< T, N > ps::generate_random_point_around	(	const Point< T, N > &	center,
		T	base_min_dist,
		std::mt19937 &	gen,
		std::function< T(const Point< T, N > &)>	scale_fn
	)

halton()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::halton	(	size_t	count,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates a set of quasi-random points using the Halton sequence in N dimensions.

This function generates count points in the unit hypercube using the Halton sequence, then rescales them to fit within the specified axis-aligned bounding box. An optional seed is used as a starting index offset (i.e., a shift) in the sequence to decorrelate multiple calls.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

count	Number of points to generate
axis_ranges	Axis-aligned bounding box for each dimension, as min/max pairs
seed	Optional seed that offsets the sequence start index

Returns

std::vector<Point<T, N>> The generated Halton points rescaled to the bounding box

Example

auto points = ps::halton<float, 2>(
    1000,
    {{{0, 1}, {0, 1}}}, 42
);

halton_sequence()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::halton_sequence	(	size_t	count,
		size_t	shift
	)

hammersley()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::hammersley	(	size_t	count,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates a set of quasi-random points using the Hammersley sequence in N dimensions.

This function generates count points in the unit hypercube using the Hammersley sequence, then rescales them to fit within the specified axis-aligned bounding box. An optional seed can be used as a starting index offset (i.e., a shift) to decorrelate multiple calls or introduce variation.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

count	Number of points to generate
axis_ranges	Axis-aligned bounding box for each dimension, as min/max pairs
seed	Optional seed that offsets the sequence start index

Returns

std::vector<Point<T, N>> The generated Hammersley points rescaled to the bounding box

Example

auto points = ps::hammersley<float, 3>(
    512,
    {{{-1, 1}, {-1, 1}, {0, 1}}}, 7
);

hammersley_sequence()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::hammersley_sequence	(	size_t	count,
		size_t	shift
	)

importance_resampling()

template<typename T , size_t N, typename DensityFn >

std::vector< Point< T, N > > ps::importance_resampling	(	size_t	count,
		size_t	oversampling_ratio,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		DensityFn	density_fn,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates a point set via importance resampling from a quasi-random oversampled grid.

This function uses a Halton sequence to create an oversampled set of candidate points in the domain. Each point is assigned a weight based on the provided density function. A discrete distribution is then used to resample count points according to these weights.

The higher the oversampling_ratio, the better the approximation to the target density, at the cost of performance.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space
DensityFn	A callable with signature T(const Point<T, N>&) returning a non-negative density value

Parameters

count	Number of points to return after resampling
oversampling_ratio	Number of candidate points to generate as a multiple of count
axis_ranges	Axis-aligned bounding box defining the domain of the points
density_fn	Function mapping a point to a (non-negative) density value
seed	Optional seed to control the random number generator

Returns

std::vector<Point<T, N>> The resulting resampled point set

Example

auto density = [](const Point<float, 2> &p) {
    return std::exp(-10.0f * (p[0]*p[0] + p[1]*p[1]));
};
 
auto points = ps::importance_resampling<float, 2>(
    500, 5,
    {{{-1, 1}, {-1, 1}}}, density, 42
);

in_neighborhood()

template<typename T , size_t N, typename ScaleFn >

bool ps::in_neighborhood	(	const GridND< T, N > &	grid,
		const Point< T, N > &	p,
		T	base_min_dist,
		const std::array< std::pair< T, T >, N > &	ranges,
		ScaleFn	scale_fn
	)

jittered_grid() [1/2]

template<typename T , size_t N>

std::vector< Point< T, N > > ps::jittered_grid	(	size_t	count,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		const std::array< T, N > &	jitter_amount,
		const std::array< T, N > &	stagger_ratio,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates a point set on a jittered and optionally staggered grid.

This function divides the domain into a grid and places one point in each selected cell. Each point is jittered within its cell, and staggered offsets may be applied depending on the index of higher-dimensional axes. The result is a semi-regular sampling pattern with randomness.

Jittering prevents aliasing, and staggering introduces a controlled shift between alternating cells to improve uniformity and avoid alignment artifacts.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

count	Number of output points (best effort, may be capped by total available cells)
axis_ranges	Axis-aligned bounding box defining the sampling domain
jitter_amount	Per-dimension jitter factor ∈ [0, 1]. A value of 1.0 means full jitter in the cell.
stagger_ratio	Per-dimension stagger ratio, indicating how much to offset points based on higher dimension parity
seed	Optional seed for deterministic jittering and shuffling

Returns

std::vector<Point<T, N>> Sampled points

Example

std::array<std::pair<float, float>, 2> bounds = {{{0.0f, 1.0f}, {0.0f, 1.0f}}};
std::array<float, 2> jitter = {0.8f, 0.8f};
std::array<float, 2> stagger = {0.2f, 0.0f};
 
auto samples = ps::jittered_grid<float, 2>(256, bounds, jitter, stagger, 42);

jittered_grid() [2/2]

template<typename T , size_t N>

std::vector< Point< T, N > > ps::jittered_grid	(	size_t	count,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates a jittered grid of points with full jitter and no stagger.

This overload defaults to jittering each dimension fully within its cell and applies no staggering. It is equivalent to calling the full version with jitter_amount filled with 1.0 and stagger_ratio filled with 0.0.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

count	Number of points to generate
axis_ranges	Axis-aligned bounding box defining the sampling domain
seed	Optional seed for deterministic jittering

Returns

std::vector<Point<T, N>> Jittered point samples

Example

std::array<std::pair<double, double>, 3> bounds = {{{0, 1}, {0, 1}, {0, 1}}};
auto points = ps::jittered_grid<double, 3>(1000, bounds, 1234);

kmeans_clustering()

template<typename T , size_t N>

std::pair< std::vector< Point< T, N > >, std::vector< size_t > > ps::kmeans_clustering	(	const std::vector< Point< T, N > > &	points,
		size_t	k_clusters,
		bool	normalize_data = true,
		size_t	max_iterations = 100
	)

Perform k-means clustering on a set of points.

Uses the dkm library to cluster points into k groups.

Template Parameters

T	Floating point type.
N	Dimensionality of the points.

Parameters

points	Vector of points to cluster.
k_clusters	Number of clusters.
max_iterations	Maximum number of iterations for k-means.

Returns

std::pair< std::vector<Point<T, N>>, std::vector<size_t> >

• First element: vector of cluster centroids.
• Second element: cluster index assignment for each point.

Example

std::vector<Point<float, 2>> pts = {
    {0.1f, 0.2f}, {0.15f, 0.22f}, {0.8f, 0.75f}
};
auto [centroids, labels] = kmeans_clustering(pts, 2);
// centroids.size() == 2
// labels.size() == pts.size()

latin_hypercube_sampling()

template<typename T , std::size_t N>

std::vector< Point< T, N > > ps::latin_hypercube_sampling	(	std::size_t	sample_count,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates samples using Latin Hypercube Sampling (LHS).

This function produces sample_count evenly stratified samples across each dimension defined in axis_ranges. Each dimension is divided into equal intervals (strata), and one point is randomly selected from each stratum with added jitter. The strata are randomly permuted across dimensions to avoid correlation.

This method ensures uniform coverage of the space while maintaining randomness, making it useful in Monte Carlo integration, surrogate modeling, and probabilistic sampling.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

sample_count	Number of points to generate
axis_ranges	Array of N (min, max) pairs defining the domain in each dimension
seed	Optional seed for reproducible randomness

Returns

std::vector<Point<T, N>> of LHS-sampled points

Example

std::array<std::pair<float, float>, 2> range = {{{0.0f, 1.0f}, {0.0f, 1.0f}}};
std::vector<Point<float, 2>> points = latin_hypercube_sampling<float, 2>(1000, range);

length()

template<typename T , size_t N>

T ps::length

(

const Point< T, N > &

a

)

length_squared()

template<typename T , size_t N>

T ps::length_squared

(

const Point< T, N > &

a

)

lerp()

template<typename T , size_t N>

Point< T, N > ps::lerp	(	const Point< T, N > &	a,
		const Point< T, N > &	b,
		T	t
	)

local_density_knn()

template<typename T , size_t N>

std::vector< T > ps::local_density_knn	(	const std::vector< Point< T, N > > &	points,
		size_t	k = 8
	)

Compute local point density based on k-nearest neighbors in N dimensions.

The density at each point is estimated as:

\[ \rho_i = \frac{k}{V_N r_i^N} \]

where (r_i) is the distance to the k-th nearest neighbor, (V_N) is the volume of the unit N-ball:

\[ V_N = \frac{\pi^{N/2}}{\Gamma(N/2 + 1)} \]

and (\Gamma) is the gamma function. This generalizes to any dimension.

Template Parameters

T	Scalar type (e.g., float, double).
N	Dimension of the points.

Parameters

points	Vector of points in N-dimensional space.
k	Number of nearest neighbors to use for density estimation (should be >= 1).

Returns

Vector of local densities for each point.

Example

std::vector<Point<double,3>> pts = ...; // 3D points
size_t k = 8;
auto densities = local_density_knn<double,3>(pts, k);

Note

• Works in any dimension (N).
• High k gives smoother density estimates, low k captures local fluctuations.
• The resulting density units are “points per unit volume” in N dimensions.

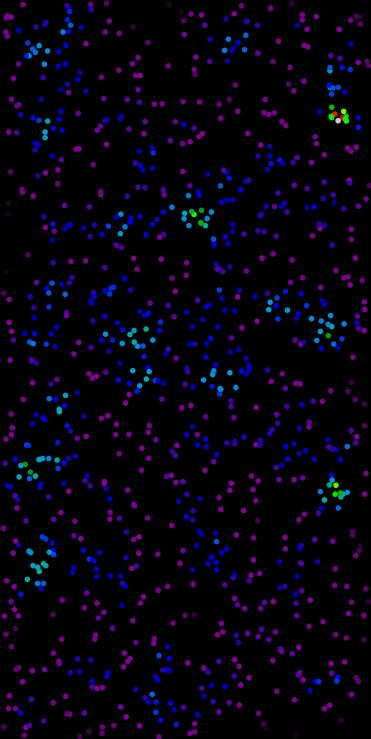
merge_by_dimension()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::merge_by_dimension

(

const std::array< std::vector< T >, N > &

components

)

Reconstructs a list of N-dimensional points from N separate coordinate vectors.

This function takes N vectors—each representing one coordinate axis—and combines them into a single vector of N-dimensional points. It is the inverse operation of split_by_dimension.

All coordinate vectors must have the same length.

For example, given:

• dimension 0: [1, 4, 7]
• dimension 1: [2, 5, 8]
• dimension 2: [3, 6, 9]

The result will be: [(1,2,3), (4,5,6), (7,8,9)]

Template Parameters

T	Scalar type (e.g., float, double).
N	Dimension of each point.

Parameters

components

An array of N vectors, each containing values for one coordinate axis.

Returns

A vector of N-dimensional points reconstructed from the coordinate vectors.

Exceptions

std::invalid_argumentifthecoordinatevectorsdonotallhavethesame

length.

Example

std::array<std::vector<float>, 3> components = {{
    {1.0f, 4.0f, 7.0f},  // x
    {2.0f, 5.0f, 8.0f},  // y
    {3.0f, 6.0f, 9.0f}   // z
}};
std::vector<Point<float, 3>> points = merge_by_dimension(components);

nearest_neighbors_indices()

template<typename T , size_t N>

std::vector< std::vector< size_t > > ps::nearest_neighbors_indices	(	const std::vector< Point< T, N > > &	points,
		size_t	k_neighbors = 8
	)

Finds the nearest neighbors for each point in a set.

This function uses a KD-tree to search for the k nearest neighbors of each point in the input set, returning their indices. The search excludes the query point itself.

Template Parameters

T	Scalar type (e.g., float, double).
N	Dimension of each point.

Parameters

points	Vector of N-dimensional points.
k_neighbors	Number of nearest neighbors to return for each point.

Returns

A vector where each element is a vector of indices representing the nearest neighbors of the corresponding point in points.

Note

The KD-tree is rebuilt internally for the search.

Example

std::vector<Point<float, 3>> points = {
    {0.0f, 0.0f, 0.0f},
    {1.0f, 0.0f, 0.0f},
    {0.0f, 1.0f, 0.0f},
    {1.0f, 1.0f, 0.0f}
};
 
auto neighbors = nearest_neighbors_indices(points, 2);
// neighbors[0] might contain {1, 2}
// neighbors[1] might contain {0, 3}

normalize_points()

template<typename T , size_t N>

void ps::normalize_points

(

std::vector< Point< T, N > > &

points

)

Normalize the coordinates of a set of points along each axis to the range [0, 1].

This function finds the minimum and maximum value for each axis across all points and rescales each coordinate so that the minimum becomes 0 and the maximum becomes 1.

Template Parameters

T	Numeric type of the coordinates (e.g., float, double).
N	Number of dimensions in each point.

Parameters

points

Vector of points to normalize. The points are modified in place.

Note

If all points have the same value along a given axis, the corresponding normalized coordinate will be set to 0 for that axis.

Example

std::vector<Point<float, 3>> points = {
    {{1.0f, 5.0f, 10.0f}},
    {{3.0f, 15.0f, 20.0f}}
};
normalize_points(points);
// Now points coordinates are scaled in [0, 1] along each axis

normalized()

template<typename T , size_t N>

Point< T, N > ps::normalized

(

const Point< T, N > &

a

)

operator*() [1/3]

template<typename T , size_t N>

Point< T, N > ps::operator*	(	const Point< T, N > &	a,
		const Point< T, N > &	b
	)

operator*() [2/3]

template<typename T , size_t N>

Point< T, N > ps::operator*	(	const Point< T, N > &	p,
		T	scalar
	)

operator*() [3/3]

template<typename T , size_t N>

Point< T, N > ps::operator*	(	T	scalar,
		const Point< T, N > &	p
	)

operator+() [1/3]

template<typename T , size_t N>

Point< T, N > ps::operator+	(	const Point< T, N > &	a,
		const Point< T, N > &	b
	)

operator+() [2/3]

template<typename T , size_t N>

Point< T, N > ps::operator+	(	const Point< T, N > &	p,
		T	scalar
	)

operator+() [3/3]

template<typename T , size_t N>

Point< T, N > ps::operator+	(	T	scalar,
		const Point< T, N > &	p
	)

operator-() [1/2]

template<typename T , size_t N>

Point< T, N > ps::operator-	(	const Point< T, N > &	a,
		const Point< T, N > &	b
	)

operator-() [2/2]

template<typename T , size_t N>

Point< T, N > ps::operator-	(	const Point< T, N > &	p,
		T	scalar
	)

operator/() [1/2]

template<typename T , size_t N>

Point< T, N > ps::operator/	(	const Point< T, N > &	a,
		const Point< T, N > &	b
	)

operator/() [2/2]

template<typename T , size_t N>

Point< T, N > ps::operator/	(	const Point< T, N > &	p,
		T	scalar
	)

percolation_clustering()

template<typename T , size_t N>

std::vector< int > ps::percolation_clustering	(	const std::vector< Point< T, N > > &	points,
		T	connection_radius
	)

Analyze percolation clusters from a set of points using a radius-based neighbor graph.

Builds a graph where edges exist if points are within connection_radius, then finds connected components (clusters).

Template Parameters

T	Scalar type (e.g., float, double).
N	Dimension.

Parameters

points	Input set of points.
connection_radius	Maximum distance for connectivity between points.

Returns

A vector of cluster labels, size = points.size(). Label = -1 if unassigned.

Example

std::vector<Point<double,2>> pts = { {0.1,0.2}, {0.15,0.22}, {0.9,0.9}};
auto labels = analyze_percolation_clusters<double,2>(pts, 0.1);
 
// labels might be {0,0,1}, meaning the first two form a cluster, third is separate.

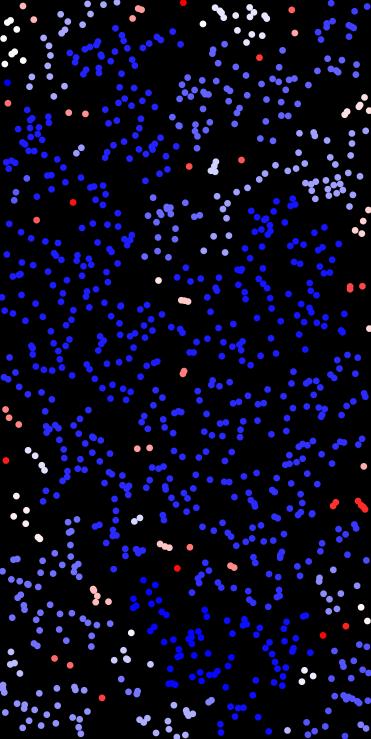
poisson_disk_sampling()

template<typename T , size_t N, typename ScaleFn >

std::vector< Point< T, N > > ps::poisson_disk_sampling	(	size_t	count,
		const std::array< std::pair< T, T >, N > &	ranges,
		T	base_min_dist,
		ScaleFn	scale_fn,
		std::optional< unsigned int >	seed = std::nullopt,
		size_t	new_points_attempts = 30
	)

Generate a set of Poisson disk samples in N-dimensional space, possibly with a warped metric.

This function uses Bridson's algorithm to generate evenly spaced points according to a minimum base distance, which can be warped using a user-defined scaling function (e.g., density or metric warping).

Template Parameters

T	Scalar type (e.g., float or double).
N	Dimension of the sampling space.
ScaleFn	Callable type returning a scaling factor at a given point.

Parameters

count	Desired number of points (will attempt to generate up to this many).
ranges	Coordinate axis ranges (bounding box) for each of the N dimensions.
base_min_dist	Base minimum distance between any two points (before scaling).
scale_fn	Function that returns a distance scaling factor at a given point. This enables warped-space or non-uniform Poisson sampling.
seed	Optional RNG seed for reproducibility.
new_points_attempts	Number of candidate points to try around each active point.

Returns

std::vector<Point<T, N>> A vector of sample points satisfying the scaled Poisson distance constraint.

Example

 auto ranges = std::array<std::pair<float, float>, 2>{{ {0.f, 1.f}, {0.f, 1.f} }};
auto scale_fn = [](const Point<float, 2> &p) -> float {
    return 1.0f + 0.5f * std::sin(p[0] * 6.2831f);  // Vary distance with x
};
auto points = poisson_disk_sampling<float, 2>(100, ranges, 0.05f, scale_fn, 42);

s

poisson_disk_sampling_distance_distribution()

template<typename T , size_t N, typename RadiusGen >

std::vector< Point< T, N > > ps::poisson_disk_sampling_distance_distribution	(	size_t	n_points,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		RadiusGen &&	radius_gen,
		std::optional< unsigned int >	seed = std::nullopt,
		size_t	max_attempts = 30
	)

Generate random points with a variable-radius Poisson disk sampling.

Radius is defined by an input distribution.

This algorithm enforces a minimum separation between points based on radii drawn from a user-specified distribution. Two points \(p_i\), \(p_j\) with radii \(r_i\), \(r_j\) must satisfy:

\[ \| p_i - p_j \| > r_i + r_j \]

This produces point sets where local spacing reflects the size distribution: many small radii yield dense clusters, while large radii produce local depletion zones.

Template Parameters

T	Scalar type (e.g. float, double).
N	Dimension of the points.
RadiusGen	Callable returning radii sampled from the target distribution.

Parameters

n_points	Number of points to generate.
axis_ranges	Ranges for each axis, defining the sampling domain.
radius_gen	Generator functor/lambda returning the next radius.
seed	Optional RNG seed for reproducibility.
max_attempts	Maximum attempts per point before giving up (controls density).

Returns

Vector of generated points satisfying the variable-radius exclusion rule.

Note

• Larger max_attempts increases the chance of filling the domain but also increases runtime.
• For efficiency, use a spatial grid or tree if generating many points.
• Radii are drawn independently per point; correlations can be introduced by adapting radius_gen.

Example

#include <random>
 
std::mt19937 rng{std::random_device{}()};
 
// 2D unit square
std::array<std::pair<double,double>,2> box = { { {0,1}, {0,1} } };
 
// Log-normal radius distribution
std::lognormal_distribution<double> logn(0.0, 0.5);
 
auto points = variable_radius_poisson_disk<double,2>(
    200,
    box,
    [&](){ return logn(rng); }
);

poisson_disk_sampling_power_law()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::poisson_disk_sampling_power_law	(	size_t	n_points,
		T	dist_min,
		T	dist_max,
		T	alpha,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		std::optional< unsigned int >	seed = std::nullopt,
		size_t	max_attempts = 30
	)

Generate N-dimensional points using Poisson disk sampling with a power-law radius distribution.

This function generates n_points in N-dimensional space such that each point is separated by a local radius sampled from a power-law distribution:

\[ p(r) \propto r^{-\alpha}, \quad r \in [\text{dist_{min}}, \text{dist_{max}}] \]

Smaller radii are more probable than larger ones, creating denser clusters with occasional larger gaps.

The sampling respects the axis ranges specified in axis_ranges and can optionally use a fixed random seed.

Template Parameters

T	Scalar type for coordinates (e.g., float, double).
N	Dimension of the space.

Parameters

n_points	Number of points to generate.
dist_min	Minimum radius for the power-law distribution.
dist_max	Maximum radius for the power-law distribution.
alpha	Power-law exponent ( \(\alpha > 0\)). Larger \(\alpha\) favors smaller distances.
axis_ranges	Array of N pairs specifying min/max range along each axis.
seed	Optional random seed for reproducibility.
max_attempts	Maximum attempts to place a point before skipping (default 30).

Returns

Vector of N-dimensional points satisfying the Poisson disk criteria with power-law distances.

Note

• Works in arbitrary dimension N.
• Uses poisson_disk_sampling_distance_distribution internally with a dynamically sampled radius.
• Smaller alpha produces more uniform spacing; larger alpha produces clustered patterns.

Example

std::array<std::pair<double,double>,3> ranges = {{{0,1},{0,1},{0,1}}};
auto points = poisson_disk_sampling_power_law<double,3>(200, 0.01, 0.2, 1.2, ranges);

poisson_disk_sampling_uniform()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::poisson_disk_sampling_uniform	(	size_t	count,
		const std::array< std::pair< T, T >, N > &	ranges,
		T	base_min_dist,
		std::optional< unsigned int >	seed = std::nullopt,
		size_t	new_points_attempts = 30
	)

Generate uniformly distributed Poisson disk samples in N-dimensional space.

This is a convenience wrapper over poisson_disk_sampling using a constant distance scale (i.e., uniform metric).

Template Parameters

T	Scalar type (e.g., float or double).
N	Dimension of the sampling space.

Parameters

count	Desired number of points (will attempt to generate up to this many).
ranges	Coordinate axis ranges (bounding box) for each of the N dimensions.
base_min_dist	Minimum distance between any two points.
seed	Optional RNG seed for reproducibility.
new_points_attempts	Number of candidate points to try around each active point.

Returns

std::vector<Point<T, N>> A vector of uniformly spaced sample points.

Example

auto ranges = std::array<std::pair<float, float>, 2>{{ {0.f, 1.f}, {0.f, 1.f} }};
auto points = poisson_disk_sampling_uniform<float, 2>(200, ranges, 0.03f, 1234);

poisson_disk_sampling_weibull() [1/2]

template<typename T , size_t N>

std::vector< Point< T, N > > ps::poisson_disk_sampling_weibull	(	size_t	n_points,
		T	lambda,
		T	k,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		std::optional< unsigned int >	seed = std::nullopt,
		size_t	max_attempts = 30
	)

Generate N-dimensional points using Poisson disk sampling with a Weibull-distributed radius.

This function generates n_points in N-dimensional space such that each point is separated by a local radius sampled from a Weibull distribution:

\[ p(r; k, \lambda) = \frac{k}{\lambda} \left(\frac{r}{\lambda}\right)^{k-1} \exp\left[-\left(\frac{r}{\lambda}\right)^k\right], \quad r \geq 0 \]

The Weibull distribution allows flexible control over radius distribution:

• Shape parameter \(k > 0\) controls skewness (e.g. \(k < 1\) heavy-tail, \(k > 1\) peaked).
• Scale parameter \(\lambda > 0\) sets the typical radius scale.

The sampling respects the axis ranges specified in axis_ranges and can optionally use a fixed random seed.

Template Parameters

T	Scalar type for coordinates (e.g., float, double).
N	Dimension of the space.

Parameters

n_points	Number of points to generate.
lambda	Scale parameter of the Weibull distribution.
k	Shape parameter of the Weibull distribution.
axis_ranges	Array of N pairs specifying min/max range along each axis.
seed	Optional random seed for reproducibility.
max_attempts	Maximum attempts to place a point before skipping (default 30).

Returns

Vector of N-dimensional points satisfying the Poisson disk criteria with Weibull-distributed distances.

Note

• Works in arbitrary dimension N.
• Uses poisson_disk_sampling_distance_distribution internally with radii sampled from Weibull distribution.
• Low shape ( \(k < 1\)) produces heavy-tailed spacing with more small radii.
• High shape ( \(k > 1\)) produces more peaked, nearly Gaussian-like spacing.

Example

std::array<std::pair<double,double>,2> ranges = {{{0,10},{0,10}}};
auto points = poisson_disk_sampling_weibull<double,2>(500, 1.0, 2.0, ranges);

poisson_disk_sampling_weibull() [2/2]

template<typename T , size_t N>

std::vector< Point< T, N > > ps::poisson_disk_sampling_weibull	(	size_t	n_points,
		T	lambda,
		T	k,
		T	dist_min,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		std::optional< unsigned int >	seed = std::nullopt,
		size_t	max_attempts = 30
	)

Poisson disk sampling in N dimensions with radii drawn from a Weibull distribution, enforcing a minimum exclusion distance.

Each point has an exclusion radius r = max(r_weibull, min_dist). The Weibull distribution is parameterized by scale λ and shape k.

Template Parameters

T	Floating-point scalar type.
N	Dimension of the space.

Parameters

n_points	Maximum number of points to attempt to place.
lambda	Weibull scale parameter (>0).
k	Weibull shape parameter (>0).
min_dist	Minimum exclusion distance enforced globally.
axis_ranges	Axis-aligned bounding box for the domain.
seed	Optional random seed.
max_attempts	Max attempts to place each point.

Returns

Vector of sampled points.

Note

• Each point is at least min_dist away from others.
• Radii are Weibull-distributed, but truncated below by min_dist.
• The effective distribution is Weibull(k, λ) left-truncated at min_dist.

example

std::array<std::pair<double,double>, 2> domain = {{{0.0, 1.0}, {0.0, 1.0}}};
auto pts = poisson_disk_sampling_weibull<double,2>(
               200, 0.2, 1.5, 0.05, domain, 42);

radial_distribution()

template<typename T , size_t N>

std::pair< std::vector< T >, std::vector< T > > ps::radial_distribution	(	const std::vector< Point< T, N > > &	points,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		T	bin_width,
		T	max_distance
	)

Compute the normalized radial distribution function g(r).

The radial distribution function (RDF) describes how the density of points varies as a function of distance from a reference point.

• g(r) ≈ 1 → uniform / random distribution at distance r
• g(r) > 1 → clustering / aggregation (excess probability of finding neighbors)
• g(r) < 1 → depletion / exclusion (points repel or avoid each other)

This function normalizes the observed pair distances against the expected density in the domain (given by axis_ranges).

Template Parameters

T	Numeric type (float, double, ...)
N	Dimension of points

Parameters

points	Vector of points
axis_ranges	Axis-aligned domain ranges for each dimension
bin_width	Width of distance bins
max_distance	Maximum distance to consider

Returns

std::pair<std::vector<T>, std::vector<T>>

• First: radii (bin centers)
• Second: normalized RDF values g(r)

Example

std::vector<Point<double, 2>> pts = {
    {0.0, 0.0}, {1.0, 0.0}, {0.0, 1.0}, {1.0, 1.0}
};
 
std::array<std::pair<double,double>,2> ranges = {
    std::make_pair(0.0, 1.0), std::make_pair(0.0, 1.0)
};
 
auto [r, g] = radial_distribution(pts, ranges, 0.1, 2.0);
 
for (size_t i = 0; i < r.size(); ++i)
  std::cout << "r=" << r[i] << " g(r)=" << g[i] << std::endl;

random()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::random	(	size_t	count,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates a specified number of uniformly distributed random points in N-dimensional space.

This function creates count random points where each coordinate is independently sampled from a uniform distribution defined by axis_ranges per dimension.

Template Parameters

T	The numeric type for coordinates (e.g., float, double).
N	The dimensionality of the points.

Parameters

count	The number of random points to generate.
axis_ranges	An array of N pairs specifying the min and max range for each axis.
seed	Optional seed for the random number generator. If not provided, a nondeterministic random seed is used.

Returns

A vector containing count randomly generated points within the specified axis ranges.

Exceptions

std::invalid_argumentIfanyaxisrangehasmin>max.

Note

The points are generated independently per axis using uniform_real_distribution.

#include <iostream>
#include "point_sampler/random.hpp"
 
int main()
{
  constexpr size_t dim = 3;
  size_t count = 5;
  std::array<std::pair<float, float>, dim> ranges = {{{0.f, 1.f},
                                                      {0.f, 2.f},
                                                      {-1.f, 1.f}}};
 
  // Generate points with a fixed seed for reproducibility
  auto points = ps::random<float, dim>(count, ranges, 42);
 
  for (const auto& p : points)
  {
    for (size_t i = 0; i < dim; ++i) std::cout << p[i] << ' ';
    std::cout << '\n';
  }
 
  return 0;
}

random_rejection_filter() [1/2]

template<typename T , std::size_t N>

std::vector< Point< T, N > > ps::random_rejection_filter	(	const std::vector< Point< T, N > > &	points,
		float	keep_fraction
	)

Randomly retains a fraction of the input points.

This is a convenience overload of random_rejection_filter that accepts a floating-point keep_fraction instead of an absolute count. Internally, it computes the number of points to retain and calls the count-based version.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

points	Input vector of points
keep_fraction	Fraction of points to retain (between 0.0 and 1.0)

Returns

std::vector<Point<T, N>> containing keep_fraction * points.size() randomly selected points

std::vector<Point<double, 3>> cloud = ps::random<double, 3>(10000,
{{-1,1},{-1,1},{-1,1}}); auto sparse = ps::random_rejection_filter(cloud, 0.25); //
Keep 25% of the points

random_rejection_filter() [2/2]

template<typename T , std::size_t N>

std::vector< Point< T, N > > ps::random_rejection_filter	(	const std::vector< Point< T, N > > &	points,
		std::size_t	target_count
	)

Randomly retains a fixed number of points from the input set.

This function returns a subset of the input points of size target_count, selected uniformly at random without replacement. If target_count is greater than or equal to the number of input points, the full input is returned.

Template Parameters

T	Scalar type (e.g., float or double)
N	Dimensionality of the space

Parameters

points	Input vector of points
target_count	Desired number of points in the output (≤ points.size())

Returns

std::vector<Point<T, N>> containing target_count randomly selected points

std::vector<Point<float, 2>> pts = ps::random<float, 2>(1000, {{0,1},{0,1}});
auto reduced = ps::random_rejection_filter(pts, 300); // Keep 300 points

random_walk_filaments()

template<typename T , size_t N>

std::vector< Point< T, N > > ps::random_walk_filaments	(	size_t	n_filaments,
		size_t	filament_count,
		T	step_size,
		const std::array< std::pair< T, T >, N > &	ranges,
		std::optional< unsigned int >	seed = std::nullopt,
		T	persistence = T(0.8),
		T	gaussian_sigma = T(0),
		size_t	gaussian_samples = 0,
		std::vector< T > *	p_distances = nullptr
	)

Generate random walk filaments in N dimensions with optional Gaussian thickness.

Each filament starts at a random seed and grows step by step, where each step is a random direction with a persistence factor to avoid sharp turns. Around each step, additional points can be sampled from a Gaussian distribution to form a "thick" filament.

Template Parameters

T	Scalar type (e.g., float, double).
N	Dimension.

Parameters

n_filaments	Number of separate filaments.
filament_count	Number of points per filament.
step_size	Average step length.
ranges	Bounding box for clamping.
seed	Optional RNG seed.
persistence	Correlation between steps (0 = totally random, 1 = straight line).
gaussian_sigma	Standard deviation of Gaussian scatter around the filament (0 = no scatter, >0 = thick filament).
gaussian_samples	Number of samples drawn per step for thickness.
p_distances	Optional output vector to store p_distances of each point from the filament center (0 for core filament points).

Returns

A vector of generated filament points.

refit_points_to_range()

template<typename T , size_t N>

void ps::refit_points_to_range	(	std::vector< Point< T, N > > &	points,
		const std::array< std::pair< T, T >, N > &	target_ranges
	)

Linearly remap a set of points to fit within the specified axis-aligned ranges.

This function computes the axis-aligned bounding box (AABB) of the input points and linearly rescales each point so that all dimensions lie in the given target_ranges.

Template Parameters

T	Numeric type (e.g., float or double).
N	Number of dimensions.

Parameters

[in,out]	points	Vector of input points to modify in-place.
[in]	target_ranges	Desired output min/max per dimension.

Example

std::vector<Point<float, 2>> pts = generate_random_points<float, 2>(100,
     { {{0.f, 1.f}, {0.f, 1.f} } }, 42);
// Refit to a new range: [10, 20] × [50, 100]
refit_points_to_range<float, 2>(pts, { { {10.f, 20.f}, {50.f, 100.f} } });

Note

If a dimension has constant value (min == max), the center of the target range is used.

rejection_sampling()

template<typename T , size_t N, typename DensityFn >

std::vector< Point< T, N > > ps::rejection_sampling	(	size_t	count,
		const std::array< std::pair< T, T >, N > &	axis_ranges,
		DensityFn	density_fn,
		std::optional< unsigned int >	seed = std::nullopt
	)

Generates random points using rejection sampling based on a user-defined density function.

This function uniformly samples candidate points within the given axis-aligned bounds and retains them based on the output of a user-provided density function. The density_fn should return a probability in the range [0, 1] for each point.

Template Parameters

T	Numeric type (e.g., float or double).
N	Number of dimensions.
DensityFn	Callable with signature T(Point<T, N>) returning a probability in [0, 1].

Parameters

count	Desired number of accepted points.
axis_ranges	Ranges for each axis in the form of an array of (min, max) pairs.
density_fn	Function that returns a probability for accepting a point.
seed	Optional seed for reproducibility.

Returns

std::vector<Point<T, N>> A vector of accepted points based on rejection sampling.

Exceptions

std::invalid_argumentifanyaxisrangeisinvalid(min>max).

Example

#include "point_sampler/rejection_sampling.hpp"
#include <iostream>
 
float radial_density(const Point<float, 2>& p)
{
    float r2 = p[0] * p[0] + p[1] * p[1];
    return std::exp(-r2); // higher near origin, drops with radius
}
 
int main()
{
    std::array<std::pair<float, float>, 2> bounds = { { {-2.0f, 2.0f},
                                                        {-2.0f, 2.0f} }};
    auto pts = ps::rejection_sampling<float, 2>(1000, bounds, radial_density, 42);
    std::cout << "Generated " << pts.size() << " points.\n";
}

Note

Rejection sampling can be inefficient if density_fn returns low values over most of the domain, as many candidate samples will be discarded.

relaxation_ktree()

template<typename T , size_t N>

void ps::relaxation_ktree	(	std::vector< Point< T, N > > &	points,
		size_t	k_neighbors = 8,
		T	step_size = T(0.1),
		size_t	iterations = 10
	)

Relax a point set using a k-nearest neighbor repulsion algorithm with a KD-tree.

This function performs iterative relaxation on a set of N-dimensional points by pushing each point away from its nearest neighbors. It uses a KD-tree for efficient neighbor lookup. The goal is to reduce clustering and obtain a more uniform or blue-noise-like distribution.

Each point is offset based on inverse-distance-weighted repulsion from its k-nearest neighbors, normalized and scaled by a step size. The point set is updated over a number of iterations.

Template Parameters

T	Numeric type for coordinates (e.g., float or double).
N	Number of dimensions.

Parameters

[in,out]	points	The point set to relax. This vector will be modified in place.
[in]	k_neighbors	Number of neighbors to consider (default is 8).
[in]	step_size	How far to move a point per iteration (default is 0.1).
[in]	iterations	Number of relaxation iterations (default is 10).

Note

The KD-tree is rebuilt on each iteration to reflect the updated positions.

Example

#include <point_sampler/relaxation.hpp>
 
std::vector<Point<float, 2>> pts = generate_random_points<float, 2>(
    1000, { { {0.f, 1.f}, {0.f, 1.f} } }, 42);
 
// Apply 10 iterations of relaxation relaxation_ktree<float, 2>(pts, 8, 0.1f, 10);

How it works:

• For each point:
  • Find its k_neighbors nearest neighbors using a KD-tree.
  • Compute offset vectors from the current point to each neighbor.
  • Weight the vectors by the inverse square distance (stronger push from closer neighbors).
  • Accumulate the offset, normalize, and scale by step_size.
  • Apply the movement to each point.
• Repeat for iterations steps.

rescale_points()

template<typename T , size_t N>

void ps::rescale_points	(	std::vector< Point< T, N > > &	points,
		const std::array< std::pair< T, T >, N > &	ranges
	)

Rescales normalized points (in [0, 1]) to specified axis-aligned ranges.

Each coordinate in every point is mapped from [0, 1] to a new range defined per axis. This is useful after generating normalized samples (e.g., Poisson disk, jittered grid).

Template Parameters

T	Numeric type (e.g., float, double).
N	Number of dimensions.

Parameters

[in,out]	points	Vector of normalized points to be modified in-place.
[in]	ranges	Target value ranges for each dimension.

std::vector<Point<float, 2>> pts = { {0.f, 0.f}, {1.f, 1.f}, {0.5f, 0.5f} };
ps::rescale_points<float, 2>(pts, { { {10.f, 20.f}, {100.f, 200.f} } });
// pts is now { {10.f, 100.f}, {20.f, 200.f}, {15.f, 150.f} }

Note

Assumes points are in [0, 1]^N. Does not check bounds.

save_points_to_csv()

template<typename T , size_t N>

bool ps::save_points_to_csv	(	const std::string &	filename,
		const std::vector< Point< T, N > > &	points,
		bool	write_header = true
	)

Save a set of N-dimensional points to a CSV file.

The output file will contain one point per line, with each coordinate separated by commas. Optionally, a header row ("x0,x1,...,xN") can be written as the first line.

Template Parameters

T	Scalar type (e.g., float, double).
N	Dimension of each point.

Parameters

filename	Path to the output CSV file.
points	Vector of points to be saved.
write_header	If true, writes a header row with column names ("x0,x1,...").

Returns

true if the file was successfully written, false otherwise.

save_vector_to_csv()

template<typename T >

bool ps::save_vector_to_csv	(	const std::string &	filename,
		const std::vector< T > &	values,
		bool	write_header = true,
		const std::string &	header_name = "value"
	)

Save a 1D vector of values to a CSV file.

This function writes a sequence of values to a CSV file with one value per row. The column name can be customized via the header_name parameter.

Template Parameters

T	Type of the values (must be streamable to std::ostream).

Parameters

filename	Path to the output CSV file.
values	The vector of values to write.
write_header	If true, writes a header line at the top of the file.
header_name	Name of the column header (only used if write_header is true).

Returns

True if the file was successfully written, false otherwise.

Note

The file will be overwritten if it already exists.

Example

std::vector<double> data = {1.0, 2.5, 3.7};
save_vector_to_csv("data.csv", data, true, "measurement");
// data.csv content:
// measurement
// 1.0
// 2.5
// 3.7

split_by_dimension()

template<typename T , size_t N>

std::array< std::vector< T >, N > ps::split_by_dimension

(

const std::vector< Point< T, N > > &

points

)

Rearranges a list of N-dimensional points into N separate coordinate vectors.

This function decomposes a vector of N-dimensional points into N vectors, where each vector contains all the values from one coordinate dimension. Useful for plotting or statistical analysis.

For example, given 3D points: [(1,2,3), (4,5,6), (7,8,9)], the result will be:

• dimension 0: [1, 4, 7]
• dimension 1: [2, 5, 8]
• dimension 2: [3, 6, 9]

Template Parameters

T	Scalar type (e.g., float, double).
N	Dimension of each point.

Parameters

points

Vector of N-dimensional points.

Returns

An array of N vectors, each containing the values for one coordinate axis.